By popular demand from certain anonymous associates of this blogging website, we thought will also cover the facet of Vedic Mathematics, as primarily written by Shankaracharya Sri Bharti Krishna Tirthaji Maharaj (1884 - 1960). However, due to the substantial amount of work he has done in compiling the earlier implicit works, done by several Vedic scholars in mathematics, we will be explaining the intricacies of these works in several parts, and their possible associations with the Vedas.

In this post we will cover Multiplication and Division.
Technique Employed
While there are several methods of Vedic origin proposed by Shankaracharya for multiplication and division, we will particularly go with the most simplistic yet powerful method in our elucidations. This method is called the Urdva-Tiryak (ऊर्ध्वतिर्यग्भ्याम्), which practically translates in English as "going vertically and cross-wise". Meaning that, in this method, the numbers are first turned into their algebraic counterparts: which is done by assigning each digit as the coefficient of its corresponding x-power, where x implicitly is the number 10, and then operating them in a vertical and cross-wise manner. Thus a number, say 1234 will be transcribed as:
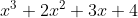
or spaced as 1 2 3 4, alternatively in order to be able to see the digits separately, and that is if the powers of 10 they belong to can be kept in mind. And this supposedly makes things easier. However, personally, I felt that working with the algebraic version to be more helpful when applying the method, because it is centered around arranging the like powers together, and then either summing them for multiplication or subtracting them for division.
A little note to make: In western terminology, this arrangement of digits into like powers before operating them, would be the infamous "divide and conquer rule" 😱, because, you know, they all just love to be so 😠😤.
Anyways, so since the Vedas back then were treated as educational material for students, and pretty much in the sense of developing their cognitive abilities, rather than cramming scientific facts, we made a search through the Vedas to see what written principles closely matched the cognitive operations for the Urdva-Tiryak method. After much effort, we found that the Sama Veda, that is particularly known for detailing ways to execute (or perform Action), to actually narrate these principles. And these were transcription, arrangement and operation. They can be found in the following places: Transcription - Sama 1:1:2:4, Arrangement - Sama 1:1:2:5 and Operation - Sama 2:5:1:2. In the next section, we will discuss this.
Sama Veda References
Transcription (Sama 1:1:2:4):

In these set of verses, it can be discerned that it places the importance of turning a task (the Agni here) into its most desirable form (as being the beloved guest of the house to be adorned with riches like that of a king's consort) that will set the path for or throw light into (the Sun beaming) getting it resolved. To do so, Mitra comes into play. Mitra, in fact is an aspect of the Sun, or Surya, that is more closely associated with Varuna. And like what we learned about Varuna in Rig Veda: The Inherent Structure of the Self, as being related to water or more precisely, a pool of pools, Mitra falls directly into this characteristic of breaking down something as complex as the Sun into its atomic but discernable parts that can further help in finding a way to resolve a problem (in our case to solve multiplication or division). Furthermore, it also mentions Kashyapa and Manu, who were the pioneers of Bharatiyan civilization [towards the end of the passage], who also employed the same principles when developing the concept of civilization. Civilization, as brought out mainly by Sage Kashyapa from the principles he learned under Sage Manu (through the Manusmriti), was the forging of a way by which people could work in different roles suitable to them and then functioning in an interconnected manner among themselves, so as to achieve a mutual benefit of growth and development (or in other words: evolution). Hence, applying the same in mathematics, we can say that the pre-algebraic transcription of the numbers before the multiplication or division operation could be a result of understanding this particular principle.
Arrangement (Sama 1:1:2:5):

Over here, we can discern the idea of steering like-entities together before any operation is undertaken. Also, more deities are involved here: Soma, Varuna, Aditya, Vishnu, Surya, Rudras, Brihaspati and even the Angirasas, onto the Agni. Now, since Soma is related to being the essential liquid or food [for the required operation], Aditya is related to compartmentalizing, Vishnu to balancing, Surya to showing light on paths, Rudras to controlling pathways, Brishaspati to making discernable connections and the Angirasas on enacting them, and this would mean that there is a clear dictum of arrangement in the passage. This arrangement is done by balancing or conserving the units. Furthermore, Manu is also mentioned again, meaning that it is actually clarifying this stance. So the vertical and cross-wise mechanism being employed for multiplication and division could actually be the simplest use case of this principle.
Operation (Sama 2:5:1:2):

In this, it is clear that some sort of filtering operation is being narrated. We also have the deities like Vayu, Asvins and Indra involved in this. We see that Vayu is being associated with Asvins, implying that they are being represented as elements (or more precisely their discernible counterparts) having specific purposes to make up the filtering operation, and Indra, here, implies the filtering towards a valuable outcome. An immediate example of this would be, say, our liver receiving the nutrients broken down by the stomach on the food we just ate, arranged through suitable chemical receptors in it, so that it can synthesize more compound nutrients, yet useful for our bodies, like proteins. That synthesis is the filter operation made using Vayu-Asvins. Likewise, in math these could be a +, - or a scaling factor, on the numbers that enter the x-power compartments. While for multiplication it employs a simple summation of numbers within the x-power compartments, for division it is the subtraction of the denominator numbers (scaled by quotient numbers) from the numerator numbers belonging to the same x-power compartments. Obviously, these filters would have been derived in such a way that achieves the desired output. However, here, we will show you only the workings of multiplication and division, and leave you to join our intensive Vedic Math Philosophy course if you wish to delve deeper.
So let's go ahead and apply them.
Multiplication
As an example for illustration, let's do 87265 x 32117. To do this let's first transform the numbers into their algebraic forms.

Now let's do the arrangement (i.e. the vertical and cross-wise) and the summations.

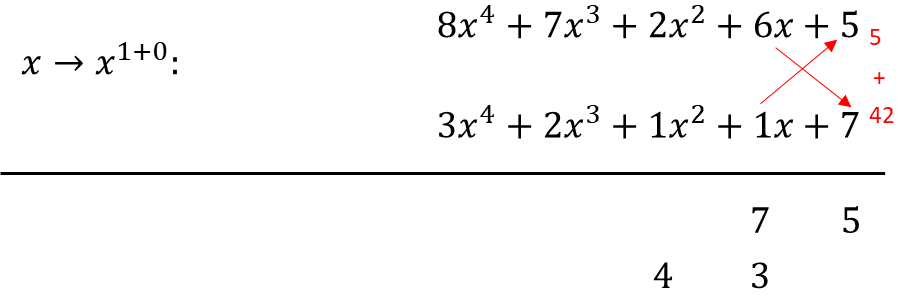
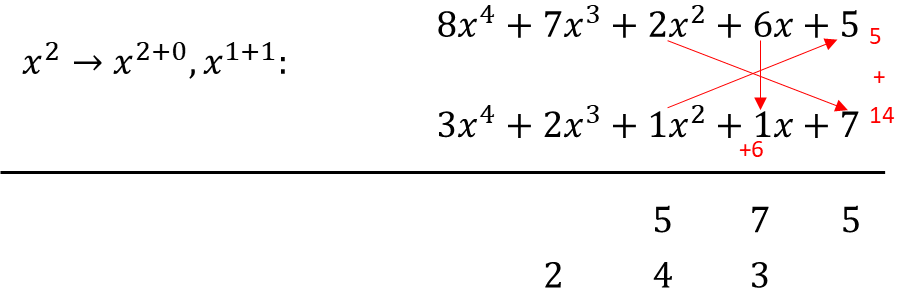
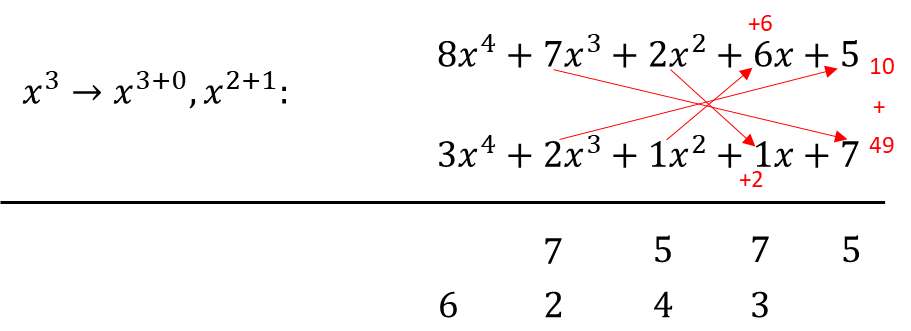
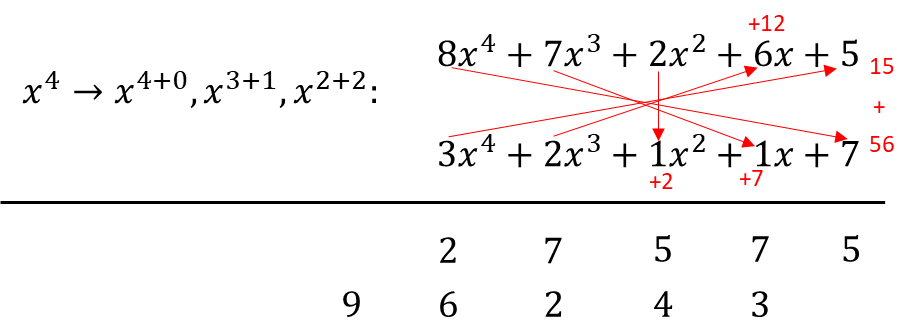
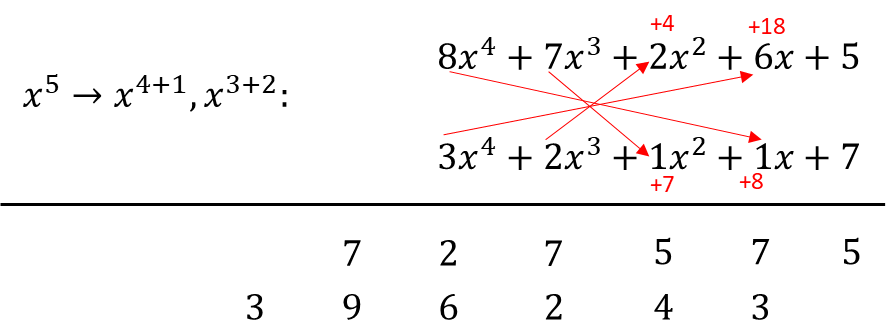
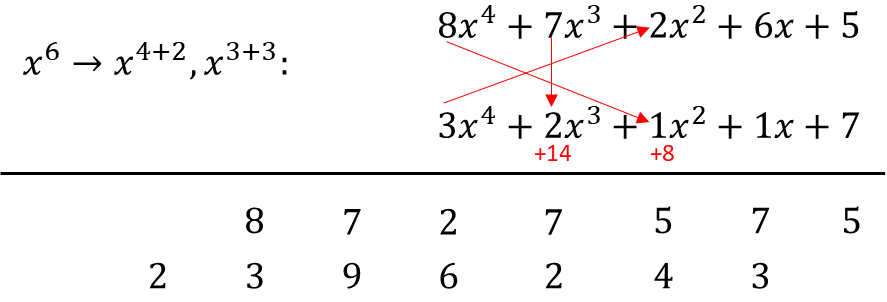
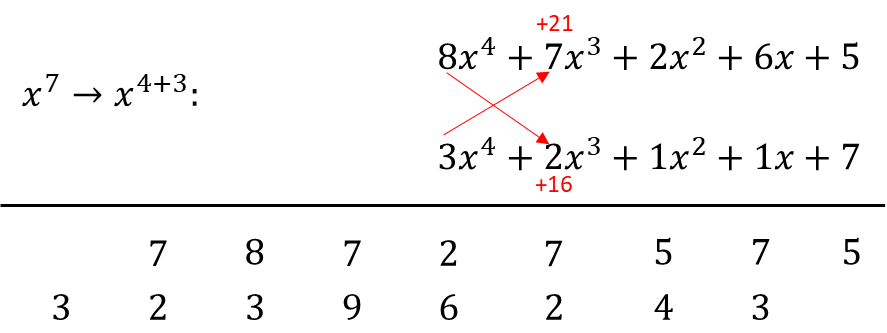
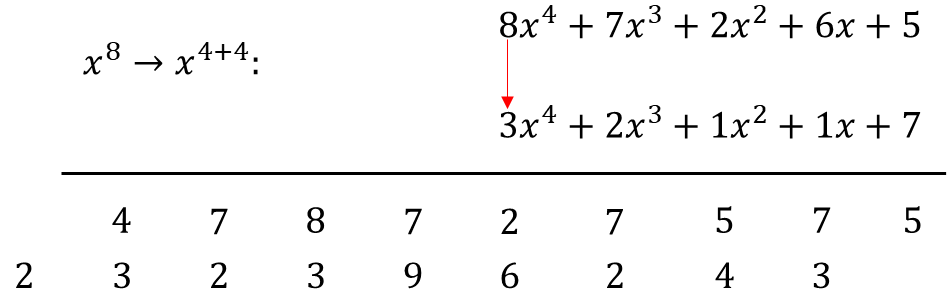
As you can see here, in just 9 easy steps, we were able to immediately come up with 2 additions, required to give us our final answer. This is opposed to the conventional method where a brute-force mechanism is typically required, which is time-consuming and cumbersome. Now let's do the addition.

And that's pretty much it.
Now in order to be able to use this method, you will only need to remember the multiplication tables until 9, that is until 9x9. Nothing more is required. And, the same can even be applied to decimal multiplication as well. You'll just have to place the decimal point in the correct location after the multiplication.
In fact, your digital calculators (or even your computers) also employ the same Urdva-Tiryak method for multiplication. It is burned right into their chips as a multiplication component. By burning, it means that the current state-of-the-art design made by elelctronics engineers today, on the circuit architecture that does the multiplication, uses this vertical and cross-wise wiring to make it happen. Did it come from Vedic mathematics? It might have. However, instead of using 10 as the x, it uses 2 because in electronics everything is dealt in binary, with only 0 and 1 as numbers.
Next, let's do division.
Division
To illustrate, lets do 1011 / 23. First lets transform.

Note here that, although we can move forward with the above algebraic division by first dividing the first terms in both the numerator and denominator, giving us a 1/2x2(square), we may try starting with an alternative transformation that can avoid this fraction. This would, without loosing anything, be:

Now if we divide the first terms, we would get 5x, which would be better to start with.
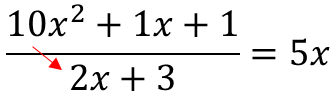
Next we multiply the 5x with the 3 and subtract from the 1x in the numerator. This will give us -14x. We then divide this with the first term in the denominator, which is 2x, to get -7. This is the usual convention to be applied if we are to obtain the correct quotient terms. We, however, don't do this for the remainder.
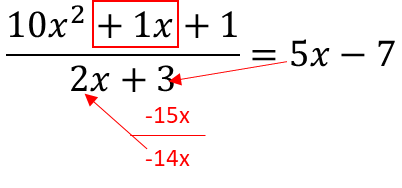
Now, let's do the same now with -7. But this time, it becomes the remainder.
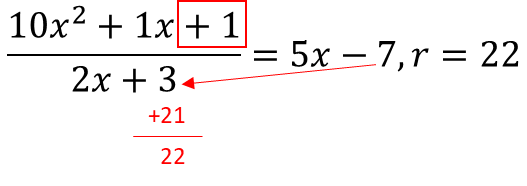
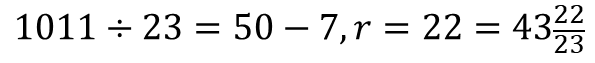
Remember, the remainder does not get divided by 2x. And voila! we have our answer in just a few simple steps. And this is without having to rack our heads each time which multiplier of 23 is needed to get closer to the remaining dividends in division, as per the conventional method. In the conventional method, we would first take the 101 in the 1011 to determine a multiplier of 23 that would come closer to the 101. If we are not equipped with the multiplication table of 23, we would have to manually search which multiplier would make the product come closer to 101, and then take it from there. We would have to do this repeatedly up until we reach the final answer. Whereas, by the Urdva-Tiryak method, we didn't have to go through all this pain at all.
Let's try another example: 13045 / 112.
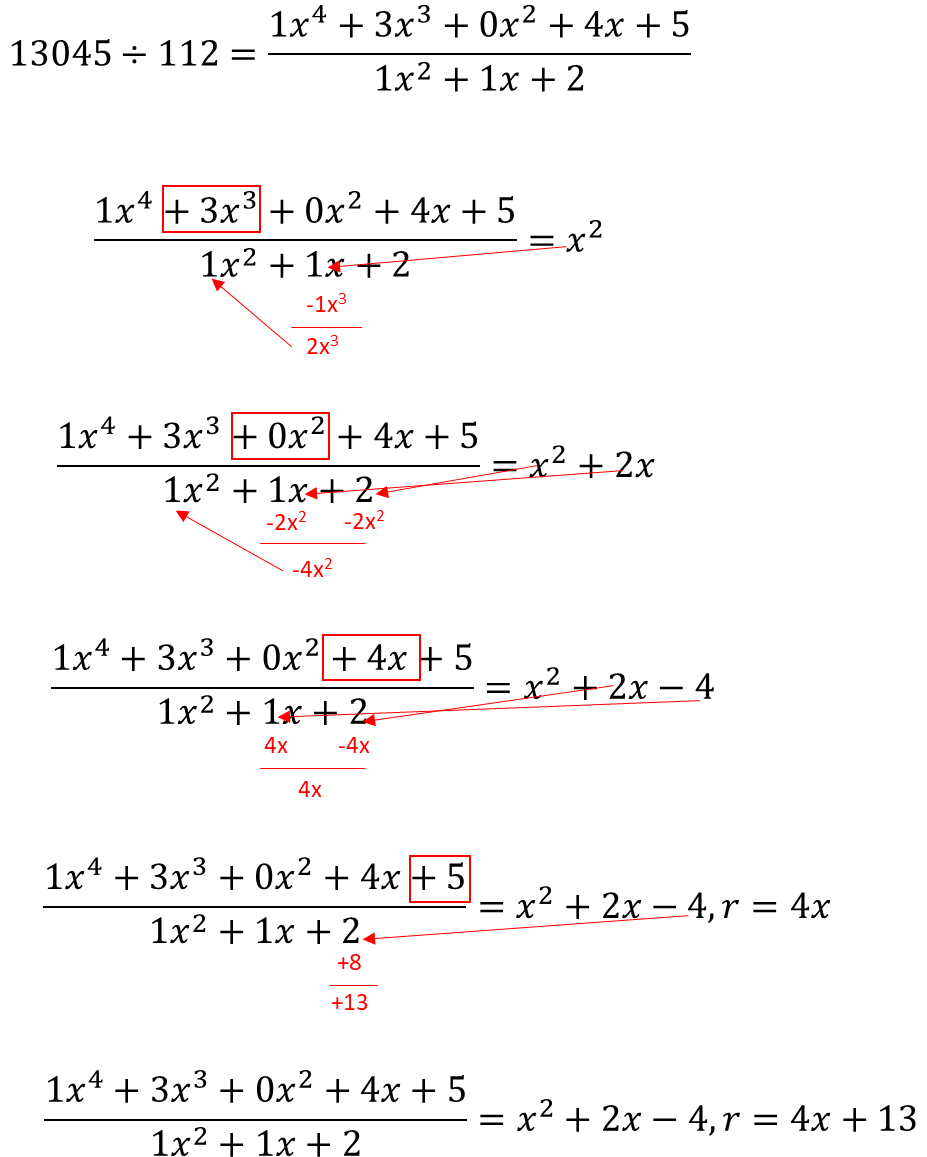
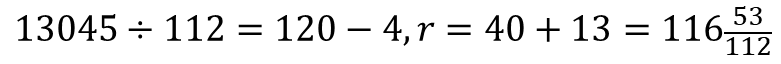
See how easy it is to do division by this method.
Remember, join our Vedic Math Philosophy program. You may also join the starter program right away through this link.
Comments